Compact \(E\)
Ensemble
séparé et dont on peut extraire un
Sous-recouvrement fini de tout
Recouvrement ouvert.
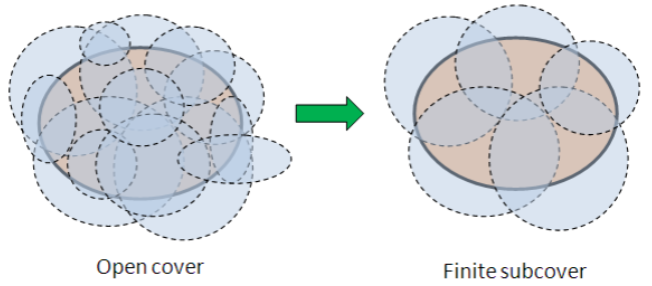
- la dernière propriété est appelée propriété de Borel-Lebesgue
- caractérisation : toute famille de Fermés sont les intersections finies sont toutes non vides a une intersection non vide
- dans un espace compact, toute intersection décroissante de fermés non vides est non vide
- \(K\subset E\) est compact s'il l'est pour la Topologie induite
- caractérisation : \(K\) est séparé et de tout recouvrement ouvert de \(K\) pour la topologie de \(E\), on peut extraire un sous-recouvrement fini
- le caractère compact se propage...
- Aux sous-ensembles Fermés
Aux intersections quelconques
Aux unions finies (dans un espace séparé)
Aux produits (pour la Topologie produit) (Théorème de Tychonov)
À l'image par une fonction continue (si l'espace d'arrivée est séparé)
- un sous-ensemble compact d'un espace séparé est fermé
- dans un espace compact, toute suite admet au moins une Valeur d'adhérence
Questions de cours
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple d'ensemble compact pour une topologie
séparée.
Verso: Tout ensemble fini fonctionne.
Bonus:
END
START
Ω Basique (+inversé optionnel)
Recto: Les ensembles munis de la
Topologie co-finie sont-ils compacts ?
Verso: Pas forcément. Ils vérifient la propriété de Borel-Lebesgue, mais ne sont pas nécessairement séparés.
Bonus:
END
START
Ω Basique (+inversé optionnel)
Recto: Dans quel cas a-t-on l'équivalence $$\text{ compact }\iff\text{ fermé borné}$$
Verso: \(\implies\) : vrai dans un
Espace métrique
\(\iff\) : vrai dans \({\Bbb R}\) (
Théorème de Heine-Borel), dans un \({\Bbb R}\)-espace vectoriel normé de dimension finie
Bonus:
END
START
Ω Basique (+inversé optionnel)
Recto: Quand a-t-on l'équivalence $$\text{ compact }\iff\text{ fermé}$$
Verso: \(\implies\) : vrai dans un espace
séparé
\(\impliedby\) : vrai dans un espace compact
Bonus:
Carte inversée ?:
END
Exercices
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple d'une somme de deux ensembles fermés d'un evn qui n'est pas fermée.
Verso:

Bonus:
Carte inversée ?:
END

